RSQとEERの関係 [投資・経済全般]
随分前のコラムになりますが、決定係数RSQと効率/標準誤差比EERとの間に、一意的な関係がありそうだということを述べました。
最近になって、システム間の相関関係を検討するに当たり、副次的に上記の疑問に解が見つかりましたのでご報告いたします。
最初に、全24個のシステムに対し、1システム当たり3通りの統計期間においてEERとRSQを求め、EERとRSQの散布図を作成しました。その結果を下図に示します。
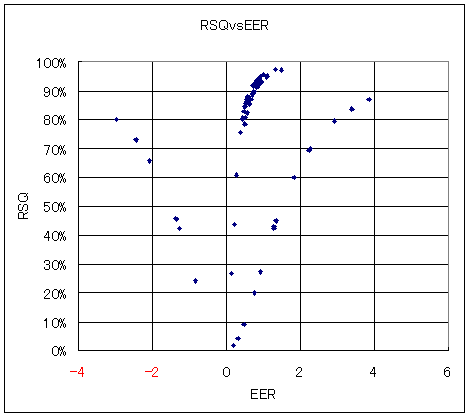
これを見ると、主に4つの系列を見て取ることができます。一つ目はEERがマイナスの領域、二つ目はそれと線対称に見えるEERがプラスの領域、三つ目は低EERでありながらRSQが高い領域で、これはよく見ると2つの系列に分かれているようです。
さて、EERは-∞~+∞の範囲の値を取るのに対し、RSQは0~1(0%~100%)の範囲の値しか取りません。RSQは時間軸に対する相関係数の2乗と等しくなりますので、RSQを相関係数に変換してみます。ただし、相関係数の符号はEERの符号と一致するものとします。
その結果を下図に示します。なお、ここでは相関係数を百分率で表示しています。
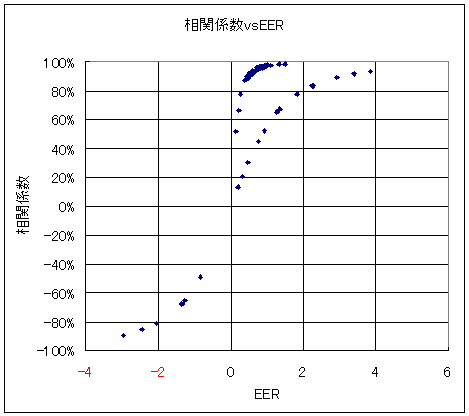
EERの正負で分かれていたラインが1本につながりました。ただし、相変わらず異なった3つの系列が残っています。
これらを融合するにはどうしたらいいのでしょう?
ここで一度、EERの定義に戻ってみます。回帰直線の傾きをa、標準誤差をδとした時、EERは次式で与えられます。
EER=365×a/δ
ここで365は1年間の日数を表しますが、別の見方をすれば、全統計期間(立会日数)の内365日(1年)分のa/δを求めている、ということです。
すなわち、このように定義されたEERは、統計期間の取り方によって値が異なってくるわけです。
そこで、EERに全統計期間/365を乗じてやれば、統計期間に依存しない、時間軸に対して規格化されたEERを求めることができます。
そうやって変換したEERをプロットし直すと、下図のようになります。
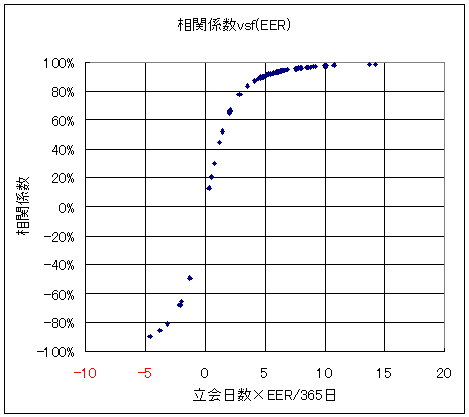
全ての系列は一つにまとまり、相関係数とEERの関係は1本の曲線で表されることが分かります。
これでめでたく、RSQとEERの関係を求めることができました。と言いたいところですが、最終的には両者の関係を数式で求める(関数化する)必要があります。
このチャートから、どのような関数形が予想できるでしょう?x軸が無限大で、y軸が±1(±100%)以内の単調増加する奇関数であることから、逆正接関数やロジスティック曲線を変換したものなどが考えられますが、闇雲に行なっても仕方がありませんので、EERやRSQの定義に戻って考えます。
まずRSQですが、これは次式で定義されます。ただし、ここでは相関係数rの2乗(r^2)として表しています。
なお、ここで使用するxは時間軸を、yは株価や資産残高を表します。また、nはデータ数です。
r^2=(n∑xy-(∑x)(∑y))^2/((n∑x^2-(∑x)^2)(n∑y^2-(∑y)^2))
また、回帰直線の傾きaと標準誤差δはそれぞれ次式で定義されます。なお、δについては、一部をRSQ(r^2)で置き換えています。
a=(n∑xy-(∑x)(∑y))/(n∑x^2-(∑x)^2)
δ=√{(n∑y^2-(∑y)^2)(1-r^2)/(n(n-2))}
ここで、Y=a/δとし、Yを計算すると、次式のようになります。
Y=√{n(n-2)/(n∑x^2-(∑x)^2)}/√{1/r^2-1}
最初の√の掛かった係数項をXとし、両辺を2乗すると、次式になります。
Y^2=X^2/(1/r^2-1)
これをrについて解くと、次のようになります。
r=±1/√{X^2/Y^2+1}
すなわち、相関係数rはEER(~a/δ=Y)を用いて、上式のように表されるわけです。
実際にXに適当な値を代入して、EERに対する相関係数をプロットしたのが、下図になります。
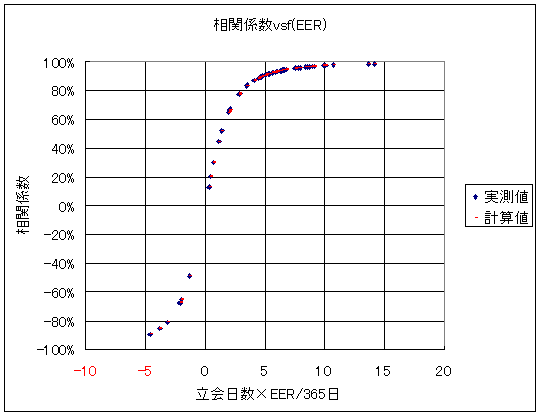
実測値と計算値とが、非常に良く一致しているのが分かるかと思います。なお、ここでrがマイナスになるのは、EERすなわちYがマイナスになる場合です。
さて、ここまでの議論では触れませんでしたが、Xは必ずしも定数ではないのではないかと言う疑問が残ります。
ちなみに、Xは次式で表されます。
X=√{n(n-2)/(n∑x^2-(∑x)^2)}
これを見ますと、何かに似ていることが分かります。そう、x(時間軸)の標準偏差σの逆数にほぼ等しいのです。ちなみに、その標準偏差σは、次式で表されます。
σ=√{(n∑x^2-(∑x)^2)/(n(n-1))}
すなわち、Xは標準偏差σを用いて次式で書けることになります。
X=√{(n-2)/(n-1)}/σ
ここで、nが大きければ√{(n-2)/(n-1)}はほとんど1と見なせますから、結局、Xは次式で表すことができます。
X=1/σ
さて、Xは定数でなければならないのですが、σはデータ数nの大きさによって異なった値となります。しかし、今までの議論の過程を振り返って見ると、そもそも系列を揃えるために、Yにデータ数nを乗じる必要があったわけですから、実質的にはXは次式で計算されることになります。
X=n/σ
これを実際に計算してみると分かりますが、Xはデータ数に拠らずほぼ一定の値になることが分かります。
そして、その結果は、4番目のチャートを作成した際に求めたXの値とほぼ一致します。
これでようやく、RSQとEERの関係を求めることができました。長い間の懸案事項だったわけですが、ようやく肩の荷が下りた感じです。
最近になって、システム間の相関関係を検討するに当たり、副次的に上記の疑問に解が見つかりましたのでご報告いたします。
最初に、全24個のシステムに対し、1システム当たり3通りの統計期間においてEERとRSQを求め、EERとRSQの散布図を作成しました。その結果を下図に示します。

これを見ると、主に4つの系列を見て取ることができます。一つ目はEERがマイナスの領域、二つ目はそれと線対称に見えるEERがプラスの領域、三つ目は低EERでありながらRSQが高い領域で、これはよく見ると2つの系列に分かれているようです。
さて、EERは-∞~+∞の範囲の値を取るのに対し、RSQは0~1(0%~100%)の範囲の値しか取りません。RSQは時間軸に対する相関係数の2乗と等しくなりますので、RSQを相関係数に変換してみます。ただし、相関係数の符号はEERの符号と一致するものとします。
その結果を下図に示します。なお、ここでは相関係数を百分率で表示しています。

EERの正負で分かれていたラインが1本につながりました。ただし、相変わらず異なった3つの系列が残っています。
これらを融合するにはどうしたらいいのでしょう?
ここで一度、EERの定義に戻ってみます。回帰直線の傾きをa、標準誤差をδとした時、EERは次式で与えられます。
EER=365×a/δ
ここで365は1年間の日数を表しますが、別の見方をすれば、全統計期間(立会日数)の内365日(1年)分のa/δを求めている、ということです。
すなわち、このように定義されたEERは、統計期間の取り方によって値が異なってくるわけです。
そこで、EERに全統計期間/365を乗じてやれば、統計期間に依存しない、時間軸に対して規格化されたEERを求めることができます。
そうやって変換したEERをプロットし直すと、下図のようになります。

全ての系列は一つにまとまり、相関係数とEERの関係は1本の曲線で表されることが分かります。
これでめでたく、RSQとEERの関係を求めることができました。と言いたいところですが、最終的には両者の関係を数式で求める(関数化する)必要があります。
このチャートから、どのような関数形が予想できるでしょう?x軸が無限大で、y軸が±1(±100%)以内の単調増加する奇関数であることから、逆正接関数やロジスティック曲線を変換したものなどが考えられますが、闇雲に行なっても仕方がありませんので、EERやRSQの定義に戻って考えます。
まずRSQですが、これは次式で定義されます。ただし、ここでは相関係数rの2乗(r^2)として表しています。
なお、ここで使用するxは時間軸を、yは株価や資産残高を表します。また、nはデータ数です。
r^2=(n∑xy-(∑x)(∑y))^2/((n∑x^2-(∑x)^2)(n∑y^2-(∑y)^2))
また、回帰直線の傾きaと標準誤差δはそれぞれ次式で定義されます。なお、δについては、一部をRSQ(r^2)で置き換えています。
a=(n∑xy-(∑x)(∑y))/(n∑x^2-(∑x)^2)
δ=√{(n∑y^2-(∑y)^2)(1-r^2)/(n(n-2))}
ここで、Y=a/δとし、Yを計算すると、次式のようになります。
Y=√{n(n-2)/(n∑x^2-(∑x)^2)}/√{1/r^2-1}
最初の√の掛かった係数項をXとし、両辺を2乗すると、次式になります。
Y^2=X^2/(1/r^2-1)
これをrについて解くと、次のようになります。
r=±1/√{X^2/Y^2+1}
すなわち、相関係数rはEER(~a/δ=Y)を用いて、上式のように表されるわけです。
実際にXに適当な値を代入して、EERに対する相関係数をプロットしたのが、下図になります。

実測値と計算値とが、非常に良く一致しているのが分かるかと思います。なお、ここでrがマイナスになるのは、EERすなわちYがマイナスになる場合です。
さて、ここまでの議論では触れませんでしたが、Xは必ずしも定数ではないのではないかと言う疑問が残ります。
ちなみに、Xは次式で表されます。
X=√{n(n-2)/(n∑x^2-(∑x)^2)}
これを見ますと、何かに似ていることが分かります。そう、x(時間軸)の標準偏差σの逆数にほぼ等しいのです。ちなみに、その標準偏差σは、次式で表されます。
σ=√{(n∑x^2-(∑x)^2)/(n(n-1))}
すなわち、Xは標準偏差σを用いて次式で書けることになります。
X=√{(n-2)/(n-1)}/σ
ここで、nが大きければ√{(n-2)/(n-1)}はほとんど1と見なせますから、結局、Xは次式で表すことができます。
X=1/σ
さて、Xは定数でなければならないのですが、σはデータ数nの大きさによって異なった値となります。しかし、今までの議論の過程を振り返って見ると、そもそも系列を揃えるために、Yにデータ数nを乗じる必要があったわけですから、実質的にはXは次式で計算されることになります。
X=n/σ
これを実際に計算してみると分かりますが、Xはデータ数に拠らずほぼ一定の値になることが分かります。
そして、その結果は、4番目のチャートを作成した際に求めたXの値とほぼ一致します。
これでようやく、RSQとEERの関係を求めることができました。長い間の懸案事項だったわけですが、ようやく肩の荷が下りた感じです。




musemistyさん、はじめまして。
nice!をいただき、ありがとうございます。
by Kフロー (2010-05-11 08:44)
hetianさん、はじめまして。
nice!をいただき、ありがとうございます。
by Kフロー (2010-05-11 11:26)
一歩前進さん、こんにちは。
いつもご覧いただき、ありがとうございます。
また、100個目のnice!をいただき、ありがとうございます。
他コラムの分とまとめて御礼申し上げます。
by Kフロー (2010-05-11 16:55)